డార్సీ సూత్రం

డార్సీ సూత్రం (ఆంగ్లం: Darcy's law) భౌతిక శాస్త్రానికి సంబంధించిన మూలసూత్రం. దీనిని హెన్రీ డార్సీ (Henry Darcy) ప్రయోగాత్మకంగా సూత్రీకరించాడు.

Diagram showing definitions and directions for Darcy's law.

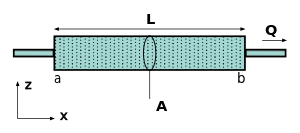
డార్సీ సూత్రాన్ని ప్రతిపాదించిన హెన్రీ డార్సీ.

డార్సీ సూత్రం

పోరస్ మాధ్యమం ద్వారా ద్రవ ప్రవాహమును వివరించే ఒక నియమిత సమీకరణం.సూత్రమును ఇసుక పడకలు ద్వారా నీటి ప్రవాహాన్ని ప్రయోగాల ఫలితాల ఆధారంగా హెన్రీ డార్సీ రూపొందించారు.డార్సీసూత్రమును ఎర్త్ సైన్సెస్ లో ఉపయోగిస్తారుమరియు ద్రవ పారగమ్యత యొక్క శాస్త్రీయ ఆధారమును ఏర్పరుస్తుంది.

వివరణ

స్థిర ఎత్తులో డార్సీ సూత్రంపోరస్ మాధ్యమం ద్వారా తక్షణ ఉత్సర్గ రేటు , ద్రవం ఘనీభవించి, ఇచ్చిన దూరంలోని ఒత్తిడి డ్రాప్ మధ్య సాధారణ అనులోమ సంబంధం.

$Q={\frac {-\kappa A}{\mu }}{\frac {(p_{b}-p_{a})}{L}}$.

ఇక్కడ Q - మొత్తం డిచ్ఛార్జ్ $\kappa$- మీడియం అంతర్గత పారగమ్యత

A - క్రాస్-సెక్షనల్ ప్రాంతము

L - ఒత్తిడి డ్రాప్ పొడవు

pb - pa - మొత్తం ఒత్తిడి డ్రాప్

μ - స్నిగ్ధత

ద్రవం అధిక ఒత్తిడి నుండి తక్కువ ఒత్తిడి సరఫరాలవలనప్రతికూల(‘-‘) సైన్ అవసరమైఉంది.ఒత్తిడి లో మార్పు ప్రతికూల ఉంటే (pa > pb ), అప్పుడు ప్రవాహం సానుకూల 'x' దిశలో ఉంటుంది.సమీకరణమును రెండు వైపులప్రాంతం ద్వారా విభజన, సాధారణ గుర్తులను ఉపయోగించి.

$q={\frac {-\kappa }{\mu }}\nabla p$,

ఇక్కడ $\nabla p$ - పీడన ప్రవణత వెక్టార్ ఇక్కడ v - ద్రవం వేగం

$v={\frac {q}{\phi }}$.

డార్సీ సూత్రం విలక్షణముగా జలమయస్తరాలలో, ప్రదర్శనలలో ప్రవహించే జలాల అనేక తెలిసిన లక్షణాల సారాంశాన్నిఇచ్చే ఒక సాధారణ గణిత ప్రకటన. . దూరం వరకు ఎటువంటి పీడన ప్రవణత ఉందనుకోండిఅప్పుడుఏ ప్రవాహం ఏర్పడధు. . పీడన ప్రవణత ఉంటే, ప్రవాహం అధిక ఒత్తిడి నుండి తక్కువ ఒత్తిడి వైపు జరుగుతుంది . ఎక్కువ పీడన ప్రవణత ఉంటె ఎక్కువ ఉత్సర్గ రేటుఉంటుంది. . అదే పీడన ప్రవణత రెండు రకాలు ఉన్నప్పటికీ ద్రవం ఉత్సర్గ రేటు తరచుగా భిన్నంగా ఉంటుంది. సాధారణంగా ఒకటి కంటే తక్కువ రేనాల్డ్స్ సంఖ్యతో ఏ ప్రవాహం స్పష్టంగా అమరుట, అది డార్సీ సూత్రంవర్తిస్తుఉంది.

$Re={\frac {\rho vd_{30}}{\mu }}$,

ఇక్కడ

ρ - నీటి సాంద్రత

V - నిర్దిష్ట ఉత్సర్గ

d₃₀ - పోరస్ మీడియా ప్రతినిధి ధాన్యం వ్యాసం

పుట్టుక

స్థిర ఫ్లోలో : $\mu \nabla ^{2}u_{i}+\rho g_{i}-\partial _{i}p=0$,

ఇక్కడ :$\mu$ - i దిశలో వేగం

$g_{i}$ - i దిశలో గురుత్వాకర్షణ భాగం ->ఒత్తిడి

$-\left(\kappa _{ij}\right)^{-1}\mu \phi u_{j}+\rho g_{i}-\partial _{i}p=0$,

ఇక్కడ $\phi$ - సారంధ్రత

$\kappa _{ij}$ - రెండవ క్రమంలో పారగమ్యత టెన్సర్

$\kappa _{ni}\left(\kappa _{ij}\right)^{-1}u_{j}=\delta _{nj}u_{j}=u_{n}=-{\frac {\kappa _{ni}}{\phi \mu }}\left(\partial _{i}p-\rho g_{i}\right)$,

ఇది N దిశలో పరిమాణ ఫ్లక్స్ సాంద్రత కోసం డార్సీసూత్రం ఇస్తుంది.

$q_{n}=-{\frac {\kappa _{ni}}{\mu }}\left(\partial _{i}p-\rho g_{i}\right)$.

సమదైశిక పోరస్ మీడియా లో పారగమ్యత టెన్సర్ ఆఫ్-వికర్ణ అంశాలు సున్నా $\kappa _{ij}=0$, $i\neq j$ వికర్ణంగా అంశాలు ఒకేలా ఉంటాయి, సాధారణ రూపం పొందవచ్చు

${\boldsymbol {q}}=-{\frac {\kappa }{\mu }}\left({\boldsymbol {\nabla }}p-\rho {\boldsymbol {g}}\right)$.