ఫిబోనాచీ సంఖ్యలు
మధ్యయుగపు యూరప్ కి చెందిన ఓ పేరుమోసిన గణితవేత్త ఫిబొనాచీ. అంకగణితము, బీజగణితము, జ్యామితి మొదలైన రంగాల్లో ఎనలేని కృషి చేశాడు. ఇతడి అసలు పేరు లియొనార్డో ద పీసా (1775-1850). ఇతడి తండ్రి బోనాచీ, ఇటాలియన్ కస్టమ్స్ అధికారిగా, దక్షిణాఫ్రికాలోని బర్గియాలో పని చేసేవాడు. (అసలు ఫిబోనాచీ అంటే బోనాచీ పుత్రుడు అని అర్థం). తండ్రి బోనాచీ ఉద్యోగ రీత్యా ఎన్నో ప్రాంతాలు తిరిగేవాడు. తండ్రితో బాటు ఫిబొనాచీ కూడా అరేబియా, ఇంకా తూర్పు ప్రాంతపు నగరాలెన్నో తిరిగాడు. ఆ యాత్రల వల్ల అతడికి హిందూ-అరబిక్ సంఖ్యా వ్యవస్థలతో గాఢమైన పరిచయం ఏర్పడింది. తను నేర్చుకోవడమే కాక వాటి వినియోగం గురించి యూరప్ లో బాగా ప్రచారం చేయటం మొదలెట్టాడు ఫిబోనాచీ. 1802 లో అతడు హిందూ-అరబిక్ సంఖ్యల గురించి ’లిబిర్ అబాచీ’ అనే పుస్తకం రాశాడు. వాటితో కూడికలు, తీసివేతలు, గుణకారాలు, భాగహారాలు మొదలైన పరికర్మలు (operations) ఎలా చెయ్యాలో అందులో వివరించాడు. అందులో ఆల్జీబ్రా, జ్యామితి కి చెందిన విస్తృత చర్చ కూడా ఉంది. ఈ కొత్త సంఖ్యా పద్ధతిని ఇటాలియన్ వర్తకులు అంత సులభంగా ఒప్పుకోలేదు. అయితే ఫిబొనాచీ తదితర యూరోపియన్ గణితవేత్తల కృషి వల్ల హిందూ-అరబిక్ సంఖ్యల వాడుక యూరప్ లో క్రమంగా పెంపొందింది.

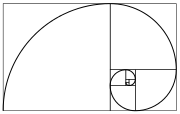
ఫిబోనాకీ సంఖ్యలు
మార్చుఫిబోనాచీ పేరు మీద ప్రస్తుతం బాగా చెలామణిలో ఉన్న ఓ సంఖ్యా శ్రేణీ లోని అంకెలు వరుసగా ఇలా ఉంటాయి.
లేదా,[1]
- అయితే ఈ శ్రేఢి ’లిబర్ అబాచీ’ లో కేవలం ఓ చిన్న లెక్క . కేవలం ఓ చిన్న అభ్యాసంలా ఇవ్వబడింది. కాని తదనంతరం 19 వ శతాబ్దంలో ఎడ్వర్డ్ లూకాస్ అనే ఫ్రెంచ్ గణితవేత్త నాలుగు భాగాల వినోద గణితం అనే గ్రంథమాలని కూర్చుతూ అందులో ఈ ఫిబోనాచీ శ్రేఢి గురించి ప్రస్తావించాడు. ’లిబర్ అబాచీ’ లో ఇవ్వబడ్డ సమస్య ఇలా ఉంటుంది.
ఫిబోనాకీ శ్రేణి-కుందేళ్ళ వృద్ధికి సామ్యం
మార్చుపునరుత్పత్తి వల్ల కుందేళ్ల జనాభా ఎలా వృద్ధి చెందుతుందో ఈ లెక్క వర్ణిస్తుంది. ఈ లెక్కలో కుందేళ్ళ జనాభా వృద్ధిని శాసించే నియమాలు ఇలా ఉంటాయి.
- ఒకే నెల వయసు ఉన్న కుందేళ్ల జంట పునరుత్పత్తికి సిద్ధంగా ఉండదు.
- కాని రెండు నెలలు వయసున్న జంట పక్వానికి వచ్చి సంతానాన్ని కంటుంది.
- రెండవ నెల నుండి నెలనెలా జంటలు సంతానాన్ని కంటాయి.
- ఆ సంతానంలో ఎప్పుడూ సరిగ్గా రెండే కూనలు (ఒక ఆడ కూన, ఒక మగ కూన) ఉంటాయి.
- కుందేళ్లకి చావు లేదు (!!!)
- ఇలా ఎదుగుతున్న కుందేళ్ళ జనాభా (కుందేళ్ళ జంటల సంఖ్య), నెల నెలా ఎలా పెరుగుతుంది అన్నదే ఈ సమస్య.
n వ నెల మొదట్లో ఉండే కుందేళ్ల జనాభా Fn అనుకుంటే, జనాభా మొదట్లో ఒక జంట మాత్రమే ఉంటుంది. కనుక F1 = 1 రెండవ నెల మొదటికి ఆ జంట పక్వానికి రాదు కనుక, రెండవ నెలలో కూడా ఒకే జంట ఉంటుంది. కనుక, F2 = 1 మూడవ నెల మొదటికి ఆ జంట పక్వానికి వచ్చి సంతానాన్ని కంటుంది. ఇప్పుడు రెండు జంటలు ఉంటాయి. F3= 2 ఇలా కుందేళ్ల జనాభా వృద్ధిని ఈ చిత్రంలో చూడొచ్చు.
ఈ శ్రేఢిలో n వ నెల జనాభా విలువ, n-1 వ, n-2 వ నెలల యొక్క జనాభా విలువల కూడిక అవుతుంది. అంటే,
F(n) = F(n-1) + F(n-2).....................(1)
మూలాలు
మార్చు- ↑ See for example Beck and Geoghegan (2010), or Bona (2011), page 180.