వర్గ సమీకరణం

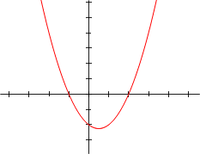The graph of a real-valued quadratic function of a real variable x, is a parabola.

${ax^{2}+bx+c=0}$ రూపంలో గల సమీరకణమును వర్గనమీకరణం అందురు. దీని పరిమాణం=2, దీనికి రెండు మూలాలు ఉంటాయి.

సాధారణ రూపం

$ax^{2}+bx+c=0,\,\!$ సమీకరణంలో ${a,b,c}$ లు చరరాశులై ${a\neq \,0}$ అయి ఉండాలి.

మూలములు కనుగొనుటకు సూత్రము

$ax^{2}+bx+c=0,\,$ వర్గ సమీకరణములో రెండు మూలములు కనుగొనుటకు ఈ సూత్రం ఉపయోగపడుతుంది.

ఈ సమీకరణము యొక్క మూలములు

$x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}},$

ఇందులో "+", " - " గుర్తులు రెండుమూలాలను కనుగొనుటకు ఉపకరిస్తాయి. అనగా

$x={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}\quad {\text{and}}\quad x={\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}$

అనునవి మూలాలు అవుతాయి.

విచక్షణి

వర్గ సమీకరణము యొక్క మూలములు కనుగొనుటకు సూత్రములో వర్గమూలంలో గల పదము అనగా ${b^{2}-4ac}$ను విచక్షణి అంటారు.దీనిని $\Delta \,$తో సూచిస్తారు.

వర్గ సమీకరణ మూలాలు ${\frac {-b+{\sqrt {\Delta \,}}}{2a}}\,$, ${\frac {-b-{\sqrt {\Delta \,}}}{2a}}\,$ అవుతాయి.

మూలాల స్వభావము

విచక్షణి విలువను బట్టి మూలాల స్వభావము

విచక్షణి ($\Delta \,$${=b^{2}-4ac}$) విలువ	మూలాల స్వభావం
$\Delta \,=0$	మూలాలు సమానములు, వాస్తవ సంఖ్యలు
$\Delta \,>0$	మూలములు అసమానములు, వాస్తవములు
$\Delta \,=<0$	మూలములు సంకీర్ణ సంఖ్యలు

మూలముల మొత్తం,లబ్దం

${ax^{2}+bx+c=0}$ వర్గసమీకరణము యొక్క మూలాలు $\alpha \,,\beta \,$ లు అయితే

మూలముల మొత్తం($\alpha \,+\beta \,$)$={\frac {-b}{a}}$
మూలముల లబ్దం ($\alpha \,\beta \,$)$={\frac {c}{a}}$

$\alpha \,,\beta \,$ లు మూలాలుగా గల వర్గ సమీకరణం

${a^{2}-(\alpha \,+\beta \,)x+\alpha \,\beta \,=0}$