బోర్ నమూనా
అణువు (atom) కైవారం ఏమాత్రం ఉంటుంది? మంచి శక్తిమంతమైన సూక్ష్మదర్శనిలో చూస్తే అణువు కనిపిస్తుందా? అణువు గ్రహాల మాదిరి గతి తప్పకుండా కేంద్రం చుట్టూ ప్రదక్షిణం చేస్తోందని అంటున్నారు కదా, ఎంత జోరుగా తిరుగుతోంది?
ఈ రకం ప్రశ్నలు పుట్టడం సహజం. అందుకని ఈ రకం ప్రశ్నలకి సమాధానాలు వెతుకుదాం. ఈ పదార్థం అర్థం అవాలంటే సంప్రదాయిక భౌతిక శాస్త్రంతో కాసింత పరిచయం ఉండాలి. గుళిక వాదం (quantum theory) లోని మజా అర్థం కావాలంటే కొంచెం శ్రమ పడి ఈ గణితం అర్థం చేసుకోవాలి.
వ్యష్టి (isolated) గా ఉన్న ఒక కేంద్రం చుట్టూ ఒకే ఒక ఎలక్ట్రాను ప్రదక్షిణం చేస్తున్నాదని ఉహించుకుందాం. ఈ రకం పరిస్థితికి ఉదజని (Hydrogen) అణువు ఒక ఉదాహరణ. ఉదజని అణువు కేంద్రకం (nucleus) లో ఒకే ఒక ప్రోటాను, దాని చుట్టూ ఒకే ఒక ఎలక్ట్రాను ప్రదక్షిణం చేస్తున్నట్లు ఉహించుకుంటాం. ఇటువంటి ఉదాహరణలు ఇంకా చాల ఉన్నాయి. మచ్చుకి - ఒక ఎలక్టరానును కోల్పోయిన రవిజని అయాను (Helium ion), రెండు ఎలక్టరానులను కోల్పోయిన లిథియం అయాను (Lithium ion).
మొదటి అంచె
మార్చుభౌతిక శాస్త్రానికి ఆయువుపట్టు శక్తి యొక్క నిక్షేప నియమం (Law of conservation energy) ప్రకారం ఎలక్ట్రాను యొక్క మొత్తం శక్తి ఖర్చు కాకుండా స్థిరంగా ఉండాలి. కేంద్రం చుట్టూ ప్రదక్షిణం చేస్తున్న ఎలక్ట్రాను యొక్క మొత్తం శక్తి - అనగా, స్థితిజ శక్తి (PE = potential energy), గతిజ శక్తి (KE = kinetic energy) - స్థిరంగా ఉండాలి. కనుక మొత్తం శక్తి (Etotal) ఎంతో ఈ దిగువ సమీకరణం రూపంలో రాస్తారు.
ఇక్కడ KE = kinetic energy అనగా గతిజ శక్తి, అనగా కదలిక వల్ల సంతరించిన శక్తి. ఇది నూటనిక సంప్రదాయపు శక్తి. దీని విలువ
పై సమీకరణంలో m అనేది ఎలక్ట్రాను భారం (mass), v అనేది ఎలక్ట్రాను యొక్క దిశవేగం (velocity). దిశవేగం అనేది వేగం (speed), దిశ (direction) రెండింటిని చెబుతుంది.
ఇప్పుడు PE = potential energy సంగతి చూద్దాం. ఇది స్థితిజ శక్తి, అనగా పరిస్థితుల ప్రభావంవల్ల సంతరించిన శక్తి. ఇక్కడ పరిస్థితులు ఏమిటి? ఎలక్ట్రానుకి ఋణ విద్యుదావేశం, కేంద్రానికి ధన విద్యుదావేశం ఉండడం వల్ల అవి పరస్పరం ఆకర్షించుకుంటాయి. ఇది కూలుంబ్ విద్యుత్ స్థితి శక్తి (Coulumb electrostatic energy). దీని విలువ
పై సమీకరణంలో q ఎలక్ట్రాను మీద ఉన్న ఆవేశం (charge), Q అన్నది కేంద్రం మీద ఉన్న ఆవేశం, r అనేది కేంద్రానికి, ఎలక్ట్రానికి మధ్య దూరం. ఒక స్థిరాంకం.
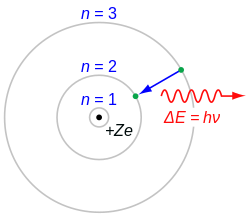
కేంద్రం మీద ఉన్న ఆవేశం ఎంత? కేంద్రంలో ఎన్ని ప్రోటానులు ఉన్నాయో దాని మీద ఆధారపడి ఉంటుంది. కేంద్రంలో ఉన్న ప్రోటానుల సంఖ్యని రివాజుగా Z అనే అక్షరంతో సూచిస్తారు. ఒకొక్క ప్రోటాను మీద ఉన్న ఆవేశం +e అనుకుంటే Q = +Ze = కేంద్రం మీద ఉన్న ఆవేశం. చుట్టూ తిరుగుతున్న ఎలక్ట్రాను మీద ఆవేశం -e.
ఇక్కడ mని కిలోగ్రాములు అనిన్నీ, vని మీటర్లు/సెకండు అనిన్ని SI మెట్రిక్ పద్ధతి ప్రకారం కొలుస్తారు. అప్పుడు గతిజ శక్తి కొలమానం కిలోగ్రాములు- (మీటర్లు/ సెకండు) (మీటర్లు/ సెకండు) అవుతుంది. దీనినే సూక్ష్మంగా “జూల్” (Joule) అంటారు. ఇప్పుడు ఎలక్ట్రాను యొక్క మొత్తం శక్తిని లెక్కకట్టటానికి ఈ దిగువ ఇచ్చిన సమాచారం సరిపోతుంది.
ఎలక్ట్రాను మీద ఉన్న ఆవేశం = కూలుంబులు
ఎలక్ట్రాను విశ్రాంతి భారం = కిలోగ్రాములు
కూలుంబ్ స్థిరాంకం = నూటన్ చదరపు మీటర్లు/వర్గు కూలుంబులు
రెండవ అంచె
మార్చుభౌతిక శాస్త్రానికి ఆయువుపట్టు అనదగిన ప్రాథమిక సూత్రం మరొకటి ఉంది. వ్యష్టిగా ఉన్న వ్యవస్థపై ప్రభావం చూపుతున్న బలాల బీజగణిత మొత్తం శూన్యం అవాలి. (The algebraic sum of the forces acting on a system must be zero.) కేంద్రం చుట్టూ ప్రదక్షిణం చేస్తున్న ఎలక్ట్రాను మీద రెండు బలాలు పనిచేస్తున్నాయి: నూటనిక బలం, కూలుంబ్ బలం. తాడుకి రాయిని కట్టి గిరగిరా తిప్పితే రాయి అపకేంద్ర బలం (centrifugal force) ప్రభావం వల్ల బయటకి లాగబడుతూ ఉంటే, ధనావేశం ఉన్న కేంద్రం ఋణావేశం ఉన్న ఎలక్ట్రానుని తనవైపు కూలుంబ్ బలంతో లాగుతూ ఉంటుంది. ఎలక్ట్రాను గతి తప్పకుండా ప్రయాణం చెయ్యాలంటే ఈ రెండు బలాలు ఒకదానిని మరొకటి రద్దు చేసుకోవాలి.
అనగా
ఈ సమీకరణంలో ఎడమ పక్క ఉన్నది అపకేంద్ర బలం, కుడి పక్క ఉన్నది విద్యుత్ స్థితి బలం, Z = 1 అయితే ఇది ఉదజని అణువుని సూచిస్తుంది. (గమనించ దగ్గ ఒక చిన్న సూక్ష్మం. కూలుంబ్ శక్తిని వర్ణించడానికి వర్ణించే సమీకరణాల్లో, హారంలో కేవలం r మాత్రమే ఉంటుంది కానీ కూలుంబ్ బలాన్ని వర్ణించేటప్పుడు దరిదాపు అదే రకం సమీకరణాల్లో, హారంలో, ఉంటుంది.)
ఈ సమీకరణం ఉపయోగించి ఎలక్ట్రాను ఎంత జోరుగా పరిభ్రమిస్తున్నాదో లెక్క కట్టడం తేలిక.
ఈ విలువని, పైన ఇచ్చిన సమాచారాన్ని తీసుకుని ఎలక్ట్రాను యొక్క మొత్తం శక్తి ఎంతో లెక్క కట్టవచ్చు. ఆ లెక్క పూర్తి చేస్తే, ఈ దిగువ చూపిన విలువ వస్తుంది.
ఇక్కడ గమనించవలసిన విషయాలు: ఎలక్ట్రాను మొత్తం శక్తి ఋణాత్మకం. కేంద్రం నుండి దూరం అవుతున్న కొద్దీ ఎలక్ట్రాను వేగం తగ్గుతుంది. మొత్తం శక్తి కూడా క్రమేణా తగ్గి, అనంతమైన దూరం వెళ్లేసరికి శూన్యం అయిపోతుంది.
మూడవ అంచె
మార్చుఈ అంచె బోర్ ప్రతిపాదనకి ఆయువుపట్టు. వేడి గుళికల మాదిరి ప్రవహిస్తోందని ప్లాంక్ అంటున్నాడు. కాంతి గుళికల మాదిరి ఉంటుందని అయిన్^స్టయిన్ అప్పటికే 1905 లో రూఢి పరచేడు. అదే బాణిలోఎలాక్ట్రాను తిరగ గలిగే గతులు (electron orbits) కూడా గుళికల సూత్రానికి బద్ధమై ఉంటాయని అనుకుంటే ఏమవుతుంది? ఇదీ బోర్ ఆలోచన. అనగా కేంద్రం నుండి ఎలక్ట్రాను గతి ఉండే దూరాన్ని గుళికీకరించాలి; అనగా కొన్ని నిర్దేశించిన దూరాలు తప్ప అన్ని దూరాలూ నిషిద్ధం. ఈ విషయాన్నే ఈ దిగువ సమీకరణం చెబుతోంది.
ఈ సమీకరణంలో ఎడమపక్క ఉన్న అంశం ఎలక్ట్రాను యొక్క కోణీయ ఉద్వేగం (angular momentum). అనేది ప్లాంక్ స్థిరాంకం మీద ఆధార పడ్డ సంక్షిప్తం (h bar అని చదువుతారు). n = 1, 2, 3,.... వగైరా పూర్ణంకాలు మాత్రమే. కనుక ఎలక్ట్రాను యొక్క కోణీయ ఉద్వేగం కొన్ని నిర్దేశించిన విలువలకి కట్టుబడి ఉండాలి. ఇక్కడ జరిగిన గుళికీకరణని ఇంగ్లీషులో, Quantization of angular momentum అని అంటారు. The angular momentum is an integer multiple of అని కూడా అంటారు.
చిన్న పిట్ట కథ: భౌతిక శాస్త్రంలోనూ, గుళిక వాదం (quantum theory) లోను కోణీయ ఉద్వేగం అనే భావానికి కీలకమైన పాత్ర ఉంది కనుక ఒక్క నిమిషం ఆగి దీని గురించి తెలుసుకుందాం. ఒక శాల్తీ గంటకి 30 కిలోమీటర్లు చొప్పున తిన్నగా ఉన్న బాట మీద నడుస్తోందని అనుకుందాం. అప్పుడు దాని వేగం (speed) గంటకి 30 కిలోమీటర్లు అని చెబుతాం. ఇదే శాల్తీ గంటకి 30 కిలోమీటర్లు చొప్పున తిన్నగా ఉన్న బాట మీద "ఉత్తర దిశ" వైపు నడుస్తోందని అనుకుందాం. అప్పుడు దాని దిశవేగం (velocity) ఉత్తర దిశగా గంటకి 30 కిలోమీటర్లు అని చెబుతాం. అనగా దిశవేగం చెప్పినప్పుడు ఏ దిశలో కదులుతున్నాదో, ఎంత వేగంగా కదులుతున్నాదో, రెండూ చెప్పాలి. ఇలా కదులుతున్న కారుని మనం చేత్తో ఆపాలని అనుకున్నాం అనుకుందాం. అంతవరకు స్థిరంగా ఉండి, అప్పుడే కదలబోతున్న కారుని ఏ కోడి రామ్మూర్తి వంటి పహిల్వానో చేత్తో ఆపెయ్యగలడు. కానీ అదే పహిల్వాను 30 కిలోమీటర్లు వేగంతో కదులుతున్న కారుని ఆపలేడు. అనగా ఎక్కువ ఊపులో ఉన్న కారుని ఆపడం కష్టము. అనగా అప్పుడే కదలబోతున్న కారు యొక్క ఊపు తక్కువ కనుక కోడి రామ్మూర్తి ఆపగలిగేడు, పరిగెడుతున్న కారు ఊపు ఎక్కువ కనుక ఆపలేకపోయాడు. ఈ ఊపు అనే భావాన్ని ఇంగ్లీషులో momentum అంటారు. దీనిని p అని ఇంగ్లీషు అక్షరంతో సూచించడం ప్రపంచ వ్యాప్తంగా ఉన్న సంప్రదాయం. దీని విలువ కదిలే వస్తువు యొక్క భారం (mass) ని, దిశవేగం (velocity) చేత గుణించగా వస్తుంది. అనగా .
ఇప్పుడు ఒక తాడుకి రాయిని కట్టి గిరగిరా తిప్పుతున్నామనుకుందాం. కారుకి బదులు రాయిని వాడేం. తిన్నగా ప్రయాణం చెయ్యడానికి బదులు రాయి గుండ్రంగా ప్రయాణం చేస్తున్నాది. ఇలా గుండ్రంగా తిరుగుతున్న రాయికి కూడా ఊపు ఉంటుంది. ఈ రకం ఊపుని ఇంగ్లీషులో angular momentum (కోణీయ ఉద్వేగం) అంటారు. ఈ ప్రపంచంలో గుండ్రంగా గిర్రున తిరిగే శాల్తీలు చాల ఉన్నాయి: బొంగరాలు, గ్రహాలు, క్షిరసాగరాలు, వగైరా. వీటన్నిటికీ కూడా కోణీయ ఉద్వేగం ఉంటుంది. ఈ కోణీయ ఉద్వేగం ఎప్పుడూ నాశనం కాదు. ఒక చోటు నుండి మరొక చోటుకి బదిలీ కావచ్చు కానీ నాశనం కాదు. దీనినే Law of Conservation of Angular Momentum అంటారు. ఇక్కడితో ఈ పిట్టకథ అయిపోయింది కానీ ఈ సూత్రం అవసరం మనకి పదేపదే వస్తుంది.
ఇప్పుడు పైన చూపిన సమాచారం సందర్భోచితంగా వాడి విలువ కట్టవచ్చు.
రెండు పక్కలా వర్గు చేసి పరిష్కరిస్తే, ఏయే విలువలు సమ్మతమో తెలుస్తుంది.
మనం అధ్యయనం చేసే అణువు ఉదజని అయితే అవుతుంది (ఉదజనిలో ఒకే ఒక ప్రోటాను ఉంది కనుక). ఇప్పుడు పై సమీకరణంలో నిర్దేశించిన విలువలని వాడి చూద్దాం. ఉదాహరణకి, అయితే ఉన్న ఒకే ఒక ఎలక్ట్రాను దూరంలో తిరుగుతూ ఉంటుంది.
ఈ సమీకరణంలో విలువలు తెలుసు కనుక విలువ కట్టగలిగేము. దీనినే బోర్ వ్యాసార్థం (Bohr radius) అంటారు.
ఇప్పుడు ఈ వ్యాసం మొదట్లో అడిగిన ప్రశ్నకి సమాధానం చెప్పొచ్చు. అనగా, ఉదజని అణువు ఎంత “పెద్దదో” ఈ వ్యాసార్థం విలువని బట్టి ఊహించవచ్చు. ఈ సంఖ్యని గుర్తు పెట్టుకోవడం ఎలా? ఇది ఉరమరగా meter లేదా 0.5 ఏంగ్^ష్ట్రం. ఈ ఏంగ్^ష్ట్రాలు SI units కావు కానీ, “అర” (½) గుర్తు ఉంచుకోవడం తేలిక. “అణువు ఎంత పెద్దగా ఉంటుంది?” అనగానే “దాని వ్యాసం ఒక ఏంగ్^ష్ట్రం ఉంటుంది” అనడం తేలిక కదా! ఏంగ్^ష్ట్రం అంటే మీటరులో పది బిలియనో వంతు.
అణువు “ఇంత” చిన్నగా ఉన్నంత మాత్రాన కంటికి ఎందుకు కనిపించకూడదు? సూక్ష్మ దర్శనిలో చూస్తే కనబడవచ్చు కదా? ఏ వస్తువు అయినా కంటికి కనబడాలంటే దాని మీద కాంతి పడి, అది ప్రతిబింబించి మన కంటిని చేరాలి. కాంతి కెరటాల పొడుగు 4000 (ఎరుపు రంగు) నుండి 7000 (ఊదా రంగు) ఏంగ్^ష్ట్రంలు ఉంటాయి. అణువు వ్యాసం ఒక ఏంగ్^ష్ట్రం ఉంటుందని ఇప్పుడే అంచనా వేసేం. కనుక అంత పెద్ద అంగలు వేసుకుంటూ పోతున్న కాంతి తరంగానికి నలుసులా ఉన్న అణువు ఆనదు. ఎలక్ట్రానుని “చూడా”లంటే బాగా పొట్టిగా ఉన్న ఏ x-కిరణాలనో వాడాలి. కానీ, అవి కంటికి కనబడవు!
నాలుగవ అంచె
మార్చుపైన ఇచ్చిన వివరణలో అయినప్పుడు ఎలక్ట్రాను “భూస్థానం” (ground state) లో ఉందని అంటారు. ఇది కనిష్ఠ శక్తి స్థానం.
ఇదే విధంగా అనుకుంటూ ఎలక్ట్రానులు తిరగ గలిగే పరిధుల దూరాలని లెక్క కట్ట వచ్చు. అవి ఉత్తేజిత శక్తి స్థానాలు (excited states) అవుతాయి.
ఇప్పుడు భూస్థానంలో ఉన్న ఎలక్ట్రానులో ఎంత శక్తి ఉందో లెక్క కడితే,
అనగా భూస్థానంలో ఉన్న (అంటే అట్ట అడుగున ఉన్న) ఎలక్ట్రాను శక్తి ఎలక్ట్రాను వోల్టులు. శక్తిని కొలవడానికి “జూల్” వాడమని SI పద్ధతి చెబుతోంది కదా, మరి ఈ ఎలక్ట్రాను వోల్టు ఎక్కడ నుండి వచ్చింది? జూల్ చాల పెద్ద కొలమానం. ఈ సందర్భానికి అనుకూలంగా ఉండే కొలత చిన్నదయిన ఎలక్ట్రాను వోల్టు. రెండు పళ్లేల మధ్య 1 ఓల్టు విద్యుత్ పీడనం అమర్చినప్పుడు ఆ క్షేత్రంలో ఒక ఎలక్ట్రాను సంతరించుకున్న శక్తిని ఒక ఎలక్ట్రాను వోల్టు ( ) అంటారు. అనగా,
- కూలుంబులు 1 ఓల్టు = జూలులు = 1 ఎలక్ట్రాను వోల్టు (eV)
ఇక్కడ అంటే కేంద్రానికి అనంతమైన దూరంలో నిశ్చలంగా ఉన్న ఎలక్ట్రాను శక్తితో పోల్చి చూస్తే భూస్థితిలో ఉన్న ఎలక్ట్రాను శక్తి ఎలక్ట్రాను వోల్టులు తక్కువ అని అర్థం. అనగా కేంద్రపు ఆకర్షక శక్తిలో చిక్కుకున్న ఎలక్ట్రాను బావిలో కప్ప లాంటిది. ఆ బావి ఆడుగు నుండి బయట పడాలంటే కప్ప శక్తిని వెచ్చించినట్లే కేంద్రపు పట్టు లోంచి బయట పడాలంటే ఎలక్ట్రాను శక్తిని వెచ్చించాలి.
అదే విధంగా అయినప్పుడు ఎలక్ట్రాను శక్తి ఎలక్ట్రాను వోల్టులు ఉంటుంది. అయినప్పుడు ఎలక్ట్రాను శక్తి ఎలక్ట్రాను వోల్టులు ఉంటుంది. అనగా, అణువు ఉద్రేకం పొంది శక్తి సంతరించుకుంటూ ఉంటే అట్టడుగున ఉన్న శక్తి స్థావరం నుండి ఎలక్ట్రాను అంచెలంచెలుగా ఊర్ధ్వ స్థాయిలలోకి వెళుతుంది. బావి లోని నీటి మట్టం భూస్థితి (ground state, n =1) లేదా “మొదటి మెట్టు “ అనుకుంటే అడుగు నుండి పైకి చూస్తున్నప్పుడు కనిపించే రెండవ మెట్టు అవుతుంది. ఆ మెట్టు మీద నుండి బయటకి పడడానికి ఎలక్ట్రాను వోల్టులు సరిపోతుంది. మూడవ మెట్టు లేదా నుండి బయటకి పడడానికి కేవలం ఎలక్ట్రాను వోల్టులు చాలు.
ఇదే విషయాన్ని మరొక విధంగా కూడా చెప్పవచ్చు. కేంద్రం పట్టు సడలించుకుని ఎలక్ట్రాను బయట పడాలంటే ఆ ఎలక్ట్రానుకి పైన చెప్పిన శక్తులు ఉండాలి. అలా కేంద్రం పట్టు విడిపించుకుని ఎలక్ట్రాను బయటకి వెళ్ళిపోతే ఆ మిగిలిన అణువుని "అయాను" (ion) అంటారు. కనుక ఈ యీ శక్తులని అయనీకరణ శక్తులు (ionization energies) అని కూడా అంటారు. రసాయన శాస్త్రంలో ఈ అయనీకరణ శక్తులు కీలకమైన పాత్ర వహిస్తాయి.
ఇప్పుడు
అనే సమీకరణాన్ని తీసుకుని ఎలక్ట్రాను దిశవేగం (velociy) ఎంతో తేలికగా లెక్క కట్టవచ్చు. అప్పుడు
వస్తుంది. ఇది కాంతి వేగంలో 10 వ వంతు. అంటే ఎలక్ట్రాను అతి జోరుగా తిరుగుతున్నాదనే కదా అర్థం అవుతోంది.
రిడ్బర్గ్ స్థిరాంకం
మార్చుపై సమీకరణంలో కనిపిస్తూన్న స్థిరాంకాలన్నిటిని కూడగట్టి ఈ కింది విధంగా రాయడం సంప్రదాయం. ఈ కింది సమీకరణంలో కనిపించే ని రిడ్బర్గ్ స్థిరాంకం అంటారు.
పైన చూపిన సమీకరణం లోని అంతరార్థం ఈ దిగువ సమీకరణాలద్వారా తెలుసుకోవచ్చు:
- is the rest mass energy of the electron (511 keV)
- is the fine structure constant
ఈ రిడ్బర్గ్ స్థిరాంకం ఉపయోగించి, ఏ శక్తి స్థావరం దగ్గర ఎంత శక్తి ఉంటుందో సాధారణీకరించి ఒక సూత్రం చూపవచ్చు:
ఈ సూత్రం "ఒక ఎలక్ట్రాను ఉన్న," "ఉదజని వంటి" ఏ అణువుకైనా వర్తిస్తుంది.
గతి మార్గాలు (orbits), శక్తి స్థావరాలు (energy levels)
మార్చుఇప్పుడు ఈ వ్యాసం మొదట్లో ఉన్న గతి మార్గాల బొమ్మ చూడండి. తరువాత ఇక్కడ ఉన్న వర్ణమాల చూడండి. ఇక్కడ ఒక ఉన్నత స్థావరం నుండి కిందికి పడినప్పుడల్లా ఎలక్ట్రాను కొంత శక్తిని కోల్పోతుంది. అలా కోల్పోయిన శక్తి ఎక్కడకి పోతుంది? ఒక తేజాణువు (ఫోటాను) ప్రకారం విడుదల అవుతుంది. అలా విడుదల అయిన ఫోటానులు ఏ యే రంగులలో కనబడతాయో బొమ్మలో చూపేను. ఇవే మనకి వర్ణమాలలో కనబడే గీతలు! వీటినే బాల్మర్ శ్రేణి గీతలు అంటారు. ఇదే సమాచారాన్ని ఎలక్ట్రాను శక్తి స్థావరాల ద్వారా కూడా చూపవచ్చు. నిజానికి శక్తి స్థావరాలు ఉపయోగించి గీసిన బొమ్మలు ఎక్కువ ప్రాచుర్యంలోఉన్నాయి.
బాల్మర్ శ్రేణి గీతలు - చారిత్రక నేపథ్యం
మార్చునీల్స్ బోర్ తన నమూనాని ప్రతిపాదించడానికి ముందే, సా . శ. 1853 లో, స్వీడన్ లోని ఉప్సల విశ్వవిద్యాలయంలో ఆచార్య ఏంగ్^ష్ట్రం ఉదజని వాయువుని ఒక గాజు గొట్టంలో బంధించి దాని గుండా విద్యుత్తు ప్రవహించేలా చేస్తే ఆ గొట్టం వెలుగులు విరజిమ్మింది. ఆ వెలుగుని వర్ణమాలాదర్శనిలో చూస్తే ఆయనకి అందులో ఎరుపు, ఆకుపచ్చ, నీలం, ఉదా రంగులతో నాలుగు గీతలు కనిపించేయి. “కనిపించేయి” అని చెప్పి ఊరుకున్నాడాయన. (పైన ఇచ్చిన బొమ్మలో ఆ గీతలని చూడవచ్చు.)
తరువాత, 1885 లో, స్విడ్జర్లండ్ లో హైస్కూలు లెక్కల మేష్టారు, జె జె బాల్మర్ అనే ఆయన, ఈ గీతలని చూసి, వాటి తరంగ సంఖ్య (wave number = 1/wave length) ల మధ్య ఒక విచిత్రమైన గణిత సంబంధం ఉన్నట్లు కనిపెట్టేడు. అందుకని ఆ గీతలకి బాల్మర్ శ్రేణి అని పేరు పెట్టేరు. ఆ గీతలు ఏమిటో, వాటి మధ్య కనిపించిన ఆ విచిత్ర గణిత సంబంధం అర్థం ఏమిటో అప్పట్లో ఎవ్వరికి అర్థం కాలేదు. బోర్ నమూనాని ఉపయోగించి ఆ గణిత సంబంధానికి భాష్యం చెప్పవచ్చు.
ముక్తాయింపు
మార్చుపైన చూపించిన బోర్ నమూనా మన ఆలోచనా సరళిలో భూకంపం అంత మార్పుకి కారణభూతమైనది కానీ ఎలక్ట్రాను ప్రవర్తన నిజానికి ఇలా ఉండదని తేలింది. అనగా బోర్ నమూనా కొత్త తరహా ఆలోచనా స్రవంతిని ప్రేరేపించినా, కొన్ని సందర్భాలలో ప్రయోగాలు ఆ నమూనాని సమర్ధించినా, ఆ నమూనా మాత్రం సరి అయినది కాదని ఋజువు అయింది. అయినా సరే ఎందుకింత శ్రమ పడి ఈ రామాయణమంతా రాయడం? ఒట్టిపోయిన ఆవుని పట్టుకు ఎంత పితికినా పాలు రాకపోవచ్చు కానీ పాలు పితకడం నేర్చుకోవచ్చు కదా. అదే విధంగా ఈ బోర్ నమూనాని ఆధారంగా చేసుకుని గుళిక శాస్త్రం లోని మెళుకువలు ఎన్నో నేర్చుకోవచ్చు.
బోర్ నమూనాకి అభ్యంతరాలు
మార్చుబోర్ నమూనా ఏవో చిన్న చిన్న విజయాలు సాధించింది కానీ ఎక్కువ కాలం నిలదొక్కుకోలేకపోయింది. బోర్ నమూనా ఆవిష్కరణ జరగక ముందే దాని పతనానికి కారణభూతమైన ప్రతికూల వాయువులు పొడచూపేయి. ఈ అభ్యంతరాలన్నీ వర్ణమాలలలో కనిపించే గీతల సూక్ష్మ శిల్పం (fine structure) కి సంబంధించినవే.
వర్ణమాలలో బొద్దు గీతలు
మార్చుబోర్ నమూనా పై మొదటి వేటు అమెరికాలో మైకెల్సన్, మోర్లే అనే ఇద్దరు శాస్త్రవేత్తలు వేసేరు. వీరిరువురు అమెరికా నుండి నోబెల్ బహుమానం అందుకున్న మొట్టమొదటివారు. అంతవరకు భౌతిక శాస్త్రంలో జరుగుతున్న విప్లవానికి కారకులైన అతిరథ మహారథులంతా ఐరోపా నుండి వచ్చినవారే. అంతవరకు నిద్రపోతున్న అమెరికా ఒళ్ళు విరుచుకుంటూ నెమ్మదిగా లేస్తోంది. ఈ సందర్భంలో, 1887లో, వీరిరువురు రెండు ప్రతిష్ఠాత్మకమైన ప్రయోగాలు చేసేరు. ఒక ప్రయోగంలో కాంతి వేగం కొలిచి అయిన్^స్టయిన్ ప్రతిపాదించిన ప్రత్యేక సాపేక్ష వాదానికి ప్రేరేపకులు అయేరు. రెండవ ప్రయోగంలో ఈ ఇద్దరు శాస్త్రవేత్తలు ఉదజని ఉద్గారించే వర్ణమాలని అధ్యయనం చేస్తూ అందులోని ఎర్ర గీత మిగిలిన గీతల కంటే కాసింత బొద్దుగా ఉన్నట్లు గమనించేరు. అది బామర్ శ్రేణి గీతలలో 3 వ శక్తి స్థావరం నుండి 2 వ శక్తి స్థావరానికి ఎలక్ట్రాను దిగజారినప్పుడు కనిపించే గీత. దాని తరంగ దైర్ఘ్యం ఉండాలి. కానీ జాగ్రత్తగా పరిశీలించి చూస్తే అక్కడ నిజానికి రెండు ఎర్ర గీతలు పక్కపక్కనే ఉన్నాయి. అందుకే అది సన్నంగా కాకుండా బొద్దుగా కనిపించింది.
బోర్ నమూనా ప్రకారం ఒక ఎలక్ట్రాను 3 వ శక్తి స్థావరం నుండి 2 వ శక్తి స్థావరానికి దిగజారినప్పుడు ఒక ఎర్ర గీత కనిపించాలి; కానీ ఇక్కడ రెండు కనబడుతున్నాయి. అనగా రెండు ఎలక్ట్రానులలో ఒకటి 3 వ శక్తి స్థావరానికి “కాసింత” పైనుండి 2 వ శక్తి స్థావరానికి దిగజారి ఉండాలి, రెండవది 3 వ శక్తి స్థావరానికి “కాసింత” కింద నుండి 2 వ శక్తి స్థావరానికి దిగజారి ఉండాలి. లేదా, బయలుదేరడం 3 వ శక్తి స్థావరం దగ్గరే బయలుదేరి, చేరడం 2 వ శక్తి స్థావరానికి “కాసింత” ఇటు అటుగా చేరి ఉండాలి. కానీ బోర్ నమూనా ప్రకారం 1 వ శక్తి స్థావరం దగ్గర, 2 వ శక్తి స్థావరం దగ్గర, 3 వ శక్తి స్థావరం దగ్గర, ఉండాలి తప్ప మధ్యేమార్గంలో “ఇటు, అటు” ఉండకూడదు. అనగా, బోర్ నమూనా మైకెల్సన్-మోర్లే ప్రయోగ ఫలితానికి కారణం చెప్పలేకపోయింది.
జీమన్ ప్రభావం
మార్చుఇది ఇలా ఉండగా, హాలండ్ లో, 1896 లో, పీట్ జీమన్ అనే పోస్ట్ డాక్టరేట్ చేస్తున్న విద్యార్థి మరొక ప్రయోగం చేసేడు. మైకెల్సన్, మోర్లే చేసినట్లే ఇతను కూడా ఉదజని ఉద్గారించే వర్ణమాలని అధ్యయనం చేస్తూ ఆ పరికరాన్ని ఒక అయస్కాంత క్షేత్రం లో పెట్టేడు. అయస్కాంత క్షేత్రం అయిన సందర్భాలలో కనిపించిన బొద్దు ఎర్ర గీత అయస్కాంత క్షేత్రం ప్రవేశ పెట్టేసరికి చిట్లిపోయి ఎన్నో ఎర్ర గీతలుగా కనిపించింది. అంతే కాదు. అయస్కాంత క్షేత్రం బలం పెరిగిన కొద్దీ ఆ చిట్లిపోయిన గీతల మధ్య దూరం పెరగడం మొదలు పెట్టింది. బోర్ నమూనా జీమన్ ప్రయోగ ఫలితానికి కారణం చెప్పలేకపోయింది.
స్టార్క్ ప్రభావం
మార్చుజర్మనీలో, 1913 లో, స్టార్క్ అనే ఆసామీ మరొక ప్రయోగం చేసేడు. ఇతను కూడా ఉదజని ఉద్గారించే వర్ణమాలని అధ్యయనం చేస్తూ ఆ పరికరాన్ని ఒక విద్యుత్ క్షేత్రం లో పెట్టేడు. విద్యుత్ క్షేత్రం అయిన సందర్భాలలో కనిపించిన బొద్దు ఎర్ర గీత విద్యుత్ క్షేత్రం ప్రవేశ పెట్టేసరికి చిట్లిపోయి ఎన్నో ఎర్ర గీతలుగా కనిపించింది. అంతే కాదు. విద్యుత్ క్షేత్రం బలం పెరిగిన కొద్దీ ఆ చిట్లిపోయిన గీతల ప్రకాశత్వం (brightness) పెరగడం మొదలు పెట్టింది. బోర్ నమూనా ఈ ప్రయోగ ఫలితానికి కారణం చెప్పలేకపోయింది.
ఇలాంటి అభ్యంతరాలు ఇంకా ఉన్నాయి. వర్ణమాలలో కనిపించే గీతలు కొన్ని ప్రకాశవంతంగాను, కొన్ని నిస్తేజంగాను ఎందుకు కనిపిస్తాయో బోర్ నమూనా చెప్పలేకపోయింది.
బోర్ నమూనాలో ఎలక్ట్రానులు కేంద్రకం చుట్టూ ఎందుకు వృత్తాకారంలోనే చక్కెర్లు కొట్టాలి? సూర్యుడి చుట్టూ గ్రహాల మాదిరి దీర్ఘవృత్తాకారంలో తిరుగుతున్నట్టు ఎందుకు ఉహించుకోకూడదు?
బోర్ నమూనా కేంద్రకం చుట్టూ ఒకే ఒక ఎలక్ట్రాను తిరుగుతున్నా సందర్భాలలోనే అన్వయిస్తుంది. మిగిలిన ఎలక్ట్రానుల మాట ఏమిటి?
మూలాలు
మార్చు- ↑ Akhlesh Lakhtakia (Ed.); Salpeter, Edwin E. (1996). "Models and Modelers of Hydrogen". American Journal of Physics. 65 (9). World Scientific: 933. Bibcode:1997AmJPh..65..933L. doi:10.1119/1.18691. ISBN 981-02-2302-1.
- వేమూరి వేంకటేశ్వరరావు, గుళిక రసాయనం (క్వాంటం కెమిస్ట్రీ), కినిగె, ఇ-పుస్తకం
- https://en.wikipedia.org/wiki/Bohr_model
- https://www.khanacademy.org/science/physics/quantum-physics/atoms-and-electrons/a/bohrs-model-of-hydrogen