స్నెల్ నియమం
స్నెల్ నియమంను స్నెల్ - డెకార్ట్ నియమము, వక్రీభవన నియమము అని కూడా అంటారు. కాంతి కిరణాలు కాని, కాంతి తరంగాలు కాని రెండు యానకాల (ఉదా: నీళ్ళు, గాలి, గాజు) మధ్యనున్న ప్రహరి (boundary) ని దాటి ప్రయాణం చేసినప్పుడు స్నెల్ నియమము పతన-వక్ర్రీభవన కోణాల మధ్య వున్న సంబంధాన్ని తెలియజేస్తుంది.[1]
కాంతి శాస్త్రంలో కిరణముల పతన, వక్రీభవన కోణాలు నిర్ణయించడానికి ఈ సూత్రాన్ని వాడతారు. ప్రయోగాత్మక కాంతి శాస్త్రంలో ఒక పదార్థము యొక్క వక్రీభవన గుణకము కనుగొనడానికి కూడా ఈ సూత్రం ఉపయోగపడుతుంది. ఈ సూత్రం "మెటామెటీరియల్స్," అనగా కాంతిని వెనక్కి వంచగలిగే పదార్థాల యెడల కూడా పనికొస్తుంది.
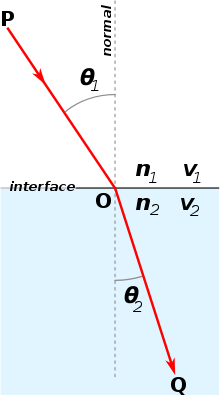
స్నెల్ సూత్రం ఏమంటుందంటే ఒక కాంతి కిరణం ఒక యానకం నుండి మరొక యానకంలోనికి ప్రయాణం చేసినప్పుడు, ఆ కిరణం యొక్క పతన కోణపు సైనుకి, వక్ర్రీభవన కోణపు సైనుకి మధ్య ఉండే నిష్పత్తి ఆయా యానకాలలో కాంతి తరంగాల దశ వేగాల నిష్పత్తితో సమానం అవడమే కాకుండా ఆయా యానకాల వక్రీభవన గుణకాలకి విలోమ నిష్పత్తిలో ఉంటాయి (బొమ్మ చూడండి). అనగా, గణిత పరిభాషలో -
ఇక్కడ అనేది పతన కిరణానికి, మాధ్యమం యొక్క లంబానికి మధ్య ఉన్న కోణం, అనేది వక్రీభవన కిరణానికి, మాధ్యమం యొక్క లంబానికి మధ్య ఉన్న కోణం, అనేది కాంతి తరంగపు దశ వేగం (en:phase velocity), అనేది మాధ్యమపు వక్రీభవన గుణకము.
ఈ నియమం ఫెర్మా సూత్రాన్ని (Fermat's principle of least time) అనుసరిస్తుంది. ఫెర్మా సూత్రం తరంగాలుగా కాంతి ప్రసరించే తీరును వివరిస్తుంది.
సాంకేతిక పదాల అర్థాలు
మార్చు- anisotropic medium = దిశానుగత యానకం
- boundary = ప్రహరి
- derivation = ఉత్పాదన
- incident angle = పతన కోణం
- index of refraction = వక్రీభవన సూచి
- isotropic medium = సమదైశిక యానకం
- medium = యానకం
- monochromatic = ఏకవర్ణ
- phase velocity = దశ వేగం
- refracted angle = వక్రీభవన కోణం
చరిత్ర
మార్చువక్రీభవన వాదం గురించి మొదటగా బాగ్దాద్ కు చెందిన ఇబ్న్ శాల్, తన పుస్తకం "ఆన్ బర్నింగ్ మిర్రర్స్ అండ్ లెన్సెస్" అనే రాత ప్రతిలో, సా. శ. 984 లో ప్రతిపాదించాడు. అతను ఈ సిద్ధాంతాన్ని కటకముల ఆకారాలని తెలుసుకొనడానికి ఉపయోగించాడు. సా. శ. 1621 లో, Willebrord Snellius (Snell) అనే శాస్త్రవేత్త గణిత శాస్త్ర ప్రకారంగా స్నెల్ నియమాన్ని రాశాడు. సా. శ. 1678 లో స్నెల్ నియమాన్ని క్రిస్టియన్ హైగెన్ (Huygens) సంపూర్ణంగా వివరించాడు.
వివరణ
మార్చుస్నెల్ సూత్రం ఉపయోగించి వివిధ వక్రీభవన గుణకములు కలిగిన మాధ్యమముల ద్వారాకాంతి కిరణాల ప్రయాణం చేసే దిశని నిర్ణయించవచ్చు. మాధ్యమముల వివిధ వక్రీభవన సూచీలను, అనగా n1, n2,....,వగైరాలని ఉపయోగించి కాంతి గమన వేగం ఆయా మాధ్యమాలలో ఎంతెంత తగ్గుతున్నాదో కనుక్కోవచ్చు.
కాంతి కిరణం ఎప్పుడైతే మాధ్యమాల మధ్య వున్న సరిహద్దు దాటుతుందో, ఆ రెండు మాధ్యమాల సాపేక్ష వక్రీభవన గుణకముల పై ఆధారపడి కాంతి కిరణం తక్కువ కోణం లేదా ఎక్కువ కోణానికి వక్రీభవించబదుతుంది. ఈ కోణాలను సరిహద్దు మీద గీసిన లంబం నుండి కొలుస్తారు. కాంతి కిరణం గాలి నుండి నీటిలోకి ప్రయాణిస్తునప్పుడు, ఆ కిరణం వాటి సరిహద్దు యొక్క లంబం వైపునకు వంగుతుంది. ఎందుకంటే కాంతి యొక్క వేగం నీటిలో తగ్గుతుంది కనుక. కాంతి కిరణం నీటిలో నుండి గాలిలోకి ప్రయాణిస్తునప్పుడు, ఆ కిరణం లంబ రేఖ నుండి దూరంగా వెళుతుంది.
స్నెల్ నియమం కేవలం సమదైశిక మాధ్యమాలకు (isotropic media) (ఉదా. గాజు) మాత్రమే వర్తిస్తుంది. దిశానుగత (anisotropic) మాధ్యమాలు (ఉదా: స్ఫటికం)లో వక్రీభవన కిరణం రెండుగా చీలిపోవచ్చు. అప్పుడు వాటిల్లో సాధారణ కిరణం (o-కిరణం) స్నెల్ సూత్రాన్ని పాటిస్తుంది కాని, అసాధారణ కిరణం (e-కిరణం) పతన కిరణం ఉన్న తలంలో ఉండకపోవచ్చు.
కాంతి కిరణాలు కాని, తదితర తరంగాలు కాని ఏకవర్ణంతో ఉన్నప్పుడు (monochromatic) లేదా ఒకే తరచుదనంతో ఉన్నప్పుడు స్నెల్ సూత్రం రెండు మాధ్యమాల తరంగదైర్ఘ్యాల ద్వారా, అనగా λ1, λ2 ల నిష్పత్తి పరంగా వ్యక్తం చేయవచ్చు.
ఉత్పాదన
మార్చుస్నెల్ సూత్రాన్ని రకరకాలుగా ఉత్పాదన చెయ్యవచ్చు
ఫెర్మా సూత్రం ఉపయోగించి
మార్చుకాంతి కిరణం దాని ప్రయాణానికి కనిష్ఠ సమయం పట్టే దారి లోనే వెళుతుందని ఫెర్మా సూత్రం చెబుతుంది.
బొమ్మలో చూపినట్లు ఒక కాంతి కిరణం Q నుండి O మీదుగా P వరకు ప్రయాణం చేసిందనుకుందాం. బిందువు Q నుండి O వరకు ప్రయాణం యానకం 1 లోనూ, O నుండి P వరకు ప్రయాణం యానకం 2 లోనూ ప్రయాణం జరిగిందని అనుకుందాం. ఈ రెండు యానకాల వక్రీభవన సూచికలు క్రమంగా , లు అనుకుందాం. మిగిలిన చలరాశులు బొమ్మ చూస్తే స్వయంబోధకాలు.
ఇప్పుడు ఈ రెండు యానకాలలోనూ కాంతి ఎంతెంత వేగాలతో ప్రయాణం చేసిందో మనం సులభంగా రాయవచ్చు:
అనేది శూన్యంలో కాంతి వేగం అనుకుందాం. ఇప్పుడు
- = మొదటి యానకంలో కాంతి వేగం
- = రెండవ యానకంలో కాంతి వేగం
ఇప్పుడు కాంతి కిరణం Q నుండి P కి ప్రయాణం చెయ్యడానికి పట్టే కాలం T అనుకుందాం.
- మొదటి యానకంలో ప్రయాణానికి పట్టే కాలం + రెండవ యానకంలో ప్రయాణానికి పట్టే కాలం
ఇప్పుడు T విలువ అత్యల్పం (minimum) అవాలంటే అవాలి.
అంతే కాకుండా, బొమ్మని బట్టి
ఈ విలువలని లో ప్రతిక్షేపిస్తే
స్నెల్ సూత్రాన్ని ఉత్పాదించడానికి ఇంకా చాలా మార్గాలు ఉన్నాయి. ఉత్సాహం, అభిరుచి ఉన్నవారు ఈ దిగువ అంశాలు సంప్రదించగలరు.
- మాక్స్వెల్ సమీకరణాలు ఉపయోగించి
- శక్తి, ద్రవ్యవేగాల విహిత నియమాలు ఉపయోగించి
- సదిశరాశులు ఉపయోగించి
ఇవి కూడా చూడుము
మార్చుబయటి లంకెలు
మార్చుమూలాలు
మార్చు- ↑ Wolf, K. B. (1995), "Geometry and dynamics in refracting systems", European Journal of Physics 16: 14–20.




